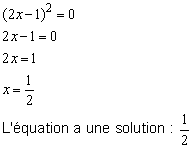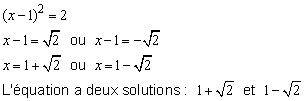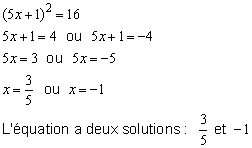-1- Définition
Soit x
un nombre positif,
la
racine carrée de x
est le nombre positif qui a pour carré ce nombre x .
La racine carrée d'un nombre négatif n'existe pas.
![]()
![]()
Exemples :
![]()
![]()
Remarque :
Si
un nombre a une racine carrée décimale alors celle-ci a deux fois moins de
zéros ou deux fois moins de chiffres après la virgule que le nombre.
Conséquences de la définition :
![]()
![]()
-2- Propriétés
Sous
réserve d'existence des nombres écrits on a toujours :
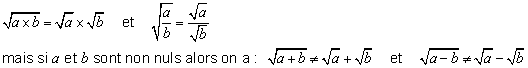
Application, simplification d'écriture,
exemples :
![]()
![]()
-3- Résolution
des équations du type :
X2 = a
Trois cas sont possibles :
1/ Si le nombre a est négatif il n'y a aucune possibilité (car
un carré n'est jamais négatif).
L'équation a zéro solution.
2/ Si le nombre a est égal à 0 il y a une seule possibilité : X = 0
3/ Si le nombre a est positif il y a deux possibilités : X = ![]() ou X = –
ou X = –![]()
Exemples :
|
|
|
|
|
|
|
|
-4- Résultats
à connaître
|
|
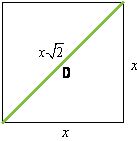
La
longueur de la diagonale d'un carré de côté x est égale à
: |
|
|
La
longueur de la diagonale d'un cube d'arrête x est égale à
: |
|
|
La
hauteur d'un triangle équilatéral de côté x est égale
à : |