Représentation graphique sur une droite graduée :
Visualisation de l’ensemble des points dont
l’abscisse x vérifie une inégalité donnée,
règle pour les crochets :
x ≥ 5 x < - 4


Si l’inégalité est écrite avec ≤ ou avec ≥ (inégalité large) la valeur extrême est permise, alors le crochet est dirigé vers le trait de couleur (crochet fermé).
Si l’inégalité est écrite avec < ou avec > (inégalité stricte) la valeur extrême est interdite, alors le crochet est dirigé vers l’extérieur (crochet ouvert).
Pour résoudre des inéquations :
(1)
|
x + a < b se traduit par: x < b – a |
Dans une inéquation on peut transposer comme dans une équation.
(2)
|
Si k est un nombre positif alors k × x < a se traduit par :
|
Si k est un nombre négatif alors k × x < a se traduit par :
Le symbole d'inégalité a changé de sens. |
Si on multiplie ou si on divise les 2 membres d’une inégalité par un même nombre négatif alors l'inégalité change de sens.
EXEMPLES :
|
3x + 5 < –7 3x < –7 – 5 3x < –12
x < - 4
|
6 – 5x ≤ – 19 – 5x ≤ – 19 – 6 – 5x ≤ – 25
x ≥ 5
Tout nombre supérieur ou égal à 5 est solution de l’inéquation. |
Inéquations simultanées, résolution de systèmes d’inéquations,
1er exemple :

|
2x – 7 ≤ 5x + 2 –7 –2 ≤ 5x – 2x –9 ≤ 3x –3 ≤ x x ≥ –3 |
4x – 1 ≤ 2x + 3 4x – 2x ≤ 3 + 1 2x ≤ 4 x ≤ 2 |
|
|
|
|
Tout nombre x tel que : –3 ≤ x ≤ 2 est solution du système. |
|
2ème exemple :

|
5 – x > 15 – 3x 3x – x > 15 – 5 2x > 10 x > 5 |
6x – 11 < 7x – 9 9 – 11 < 7x – 6x –2 < x x > –2 |
|
|
|
|
Tout nombre x tel que : x > 5 est solution du système. |
|
3ème exemple :
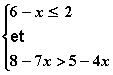
|
6 – x ≤ 2 – x ≤ 2 –6 – x ≤ –4 x ≥ 4 |
8 – 7x > 5 – 4x 8 – 5 > 7x – 4x 3 > 3x 1 > x x < 1 |
|
|
|
|
Le système n’a pas de solution. |
|


