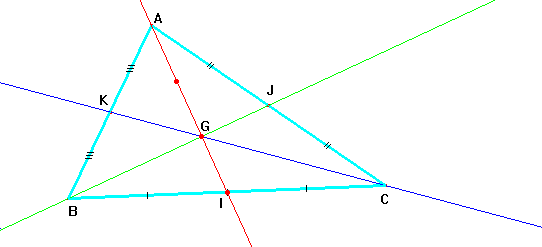

DÉFINITION
: Une médiane dans un triangle est une droite passant par un sommet et par le milieu du côté opposé.PROPRIÉTÉ
: Dans un triangle les 3 médianes sont toujours concourantes. Leur point commun est appelé centre de gravité du triangle. Il est situé sur chaque médiane aux deux tiers à partir du sommet:![]()
REMARQUE
: Le centre de gravité d'un triangle est toujours à l'intérieur de ce triangle.|
|
|
DÉFINITION
: Une hauteur dans un triangle est une droite passant par un sommet et perpendiculaire au côté opposé.PROPRIÉTÉ:
Dans un triangle les 3 hauteurs sont toujours concourantes. Leur point commun est appelé orthocentre du triangle.REMARQUE
: Quand le triangle a 3 angles aigus l'orthocentre est à l'intérieur du triangle, quand le triangle a un angle obtus l'orthocentre est à l'extérieur du triangle.|
|
|
DÉFINITION
: La médiatrice d'un segment est la perpendiculaire à ce segment en son milieu.RAPPEL
: la médiatrice d'un segment est aussi l'ensemble des points équidistants des extrémités du segment.PROPRIÉTÉ
: Les médiatrices des 3 côtés d'un triangle sont toujours concourantes. Leur point commun est le centre du cercle passant par les 3 sommets du triangle, c'est à dire le centre du cercle circonscrit au triangle.REMARQUE
: Quand le triangle a 3 angles aigus le centre du cercle circonscrit est à l'intérieur du triangle, quand le triangle a un angle obtus le centre du cercle circonscrit est à l'extérieur du triangle.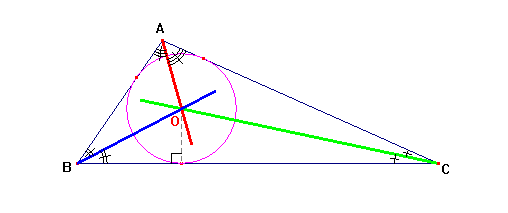
DÉFINITION
: La bissectrice d'un angle est la demi-droite issue du sommet, qui partage l'angle en 2 angles de même mesure. (La demi-droite qui partage l'angle en 2 angles égaux et adjacents.)RAPPEL
: La bissectrice d'un angle est aussi son axe de symétrie.PROPRIÉTÉ
: Les bissectrices des 3 angles d'un triangle sont toujours concourantes. Leur point commun est le centre du cercle tangent aux 3 côtés du triangle, c'est à dire le centre du cercle inscrit dans le triangle.REMARQUE
: Le centre du cercle inscrit est toujours à l'intérieur du triangle.-5- CAS PARTICULIERS
Dans un triangle quelconque il y a
12 droites remarquables, parfois certaines de ces droites sont confondues:|
Dans un triangle isocèle il existe une droite qui est à la fois médiane, hauteur, médiatrice, bissectrice. Pour qu'un triangle soit isocèle il suffit qu'une même droite joue 2 de ces rôles à la fois. Cette droite est alors aussi l'axe de symétrie du triangle isocèle.
|
Dans un triangle équilatéral les trois médianes sont aussi les trois hauteurs, les trois médiatrices, les trois bissectrices et les trois axes de symétrie.
|